DERIVADA DEL COCIENTE

La derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador menos la derivada del denominador por el numerador, divididas por el cuadrado del denominador.

ejm:

DERIVADA DE UN PRODUCTO

La derivada del producto de dos funciones es igual al primer factor por la derivada del segundo factor por la derivada del primero

ejm:

DERIVADA DE UNA SUMA

La derivada de una suma dedos funciones es igual a la suma de las derivadas de dichas funciones

Esta regla se extiende a cualquier numero de sumandos, ya sea positivo o negativo.

ejm:

DERIVADA DE UNA POTENCIA

La derivada de un potencia o una funcion potencial, es igual al exponente por la base elevada al exponente menos uno y por la derivada de la base

Si la base es la funcion identidad, la derivada es igual al exponente por la base elevada al exponente menos uno.

ejm:

DERIVADA DE UNA CONSTANTE

Aclaremos que una constante puede ser un numero o una letra. Es el termino que no tiene x

La derivada de una constante es cero

f(x)=k f '(x)= 0

ejemplo: f(x)= -2 f '(x)= 0

f(x)=9 f '(x)=0

PENDIENTE Y ECUACION DE LA RECTA TANGENTE

La pendiente es la inclinacion de una recta. Una forma de calcular la pendiente usando la siguiente formula. Dados dos puntos (X1, Y1)(X2,Y2) que estan en una recta l, la inclinacion o la pendiente m se determina mediante:

m= Y2-Y1
_____
X2- X1

LA PENDIENTE DE LA RECTA TANGENTE A UNA CURVA EN UN PUNTO ES LA DERIVADA DE LA FUNCION EN DICHO PUNTO.

EJEMPLO: BUSCAR LA PENDIENTE DE LOS PUNTOS: (2,4) y (3,6)

m= Y2-Y1 6-4 2
_____ =___= __ = 2
X2-X1 3-2 1

LA PENDIENTE ES 2

Aveces tenemos dos puntos y queremos hallar la ecuacion de la recta que pasa por estos puntos. Primero hay que determinar la pendiente de la recta y para hallar la ecuacion, utilizamos la ecuacion y=mx+b donde m es la pendiente de la recta y b es el intercepto de b.

ejm: Buscar la ecuacion de la recta que pasan por los puntos (1,5 ) y (0,9)

m= Y2-Y1 9-5 4
_____ = ____ = __ = -4
X2-X1 0 -1 -1

La pendiente es -4 ahora hay que buscar el intercepto en y en este caso ya esta dado por 0.9.

Si la pendiente es -4 y el intercepto es 0,9 entonces la ecuacion es

y= -4x+9

Nota: Para buscar el intercepto y hay que siempre fijarse que la ecuacion esteen su forma y=mx+b. si no lo esta hay que expresarla respecto a y.
ejemplo: 9x-3y=12
-3y=-9x+12

-3y -9x + 12
__ = __ = __ YA ESTA EN LA FORMA y=mx+b Y SU INTERCEPTO
-3 -3 -3 EN Y ES -4

y= 3x-4

PERSONAJES QUE INFLUYERON EN LAS DERIVADAS

PIERRE DE FERMANT

(1601- 1665)

Matematico frances, poco se conoce de sus primeros años, exepto que estudio derecho,posiblemente en Touluse y Burdeos. Interesado por las matematicas , en 1629 abordo la tarea de reconstruir las demostraciones perdidas del matematico Apolonio relativas a los lugares geometricos; a tal efecto desarrolllaria, contemporanea e independientemente de RENE DESCARTES, un metodo algebraico para tratar cuestiones geometricas por medio de un sistema de coordenadas.

Diseño tambien un algoritmo de diferenciacion mediante el cual pudo determinar los valores maximos y minimos,de una curva polinomica, para trazar las correspondientes tangentes, logros todos ellos que abrieron el camino al desarrollo unteriol del calculo infinitestimal de NEWTON y LEIBNIZ . Tras a sumir que cuando la luz se desplaza en un medio mas denso, su velocidad disminuye, demostro que el camino luminoso entre dos puntos es siempre aquel que le cuesta menos tiempo en recorrer; de dicho principio, que lleva su nombre, se deducen las leyees de la reflexion y la refraccion.

ISAAC NEWTON

(1642- 1727)

Suele considerarsele uno de los protagonistas principales de la llamada REVOLUCION CIENTIFICA.

del siglo XVII

Considio con Leibnitz en el descubrimiento del calculo integral,que contribuiria a una profunda renovacion de las matematicas; tambien formulo el teorema del binomio, pero sus aportes escenciales se dieron en la fisica.

Tambien trabajo en otras areas como la termodinamica, y la acustica pero su lugar en la historia de la ciencia se debe a la refundacion de la mecanica en su obra mas importante PRINCIPIOS MATEMATICOS DE LA FILOSOFIA NATURAL

Formulo las tres leyes fundamentales del movimiento como son: la inercia, dinamica y accion- reaccion.Y de estas dedujo la cuarta mas importante que es la gravedad.

LEIBNIZ
(146-1716)

Filosofo y matematico aleman.

Las contribuciones en el campo del calculo infinitestimal, efectuadas con independencia de los trabajos de NEWTON, asi como en el ambito del analisis, combinatorio fueron de enorme valor. Introdujo la notacion actualmente utilizada en el calculo diferencial e integral. Los trabajos que realizo en su juventu,la busquedad de unlenguaje perfecto que reformara toda la ciencia y permitiese convertir la logica en un calculo, acabaron por desempeñar un papel desicivo en la fundacion de la moderna logica simbolica.

MICHEL ROLLE

(1652-1719)

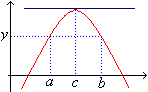
Se dio cuenta de que si tomamos dos valores de una funcion que tengan la misma imagen, debemos encontrar dentro del mismo intervalo (que tiene a los dos valores como extremos del intervalo) un valor de x, al que cuya c, cuya tangente sea paralela al eje x, osea tenga pendiente nula. Es interesante destacar que ese valor siempre es el punto medio del segmeto ab, por lo que se le conose como teorema del valor medio(aunque pueda sonar redundante, hay que destacar que el intervalo ab es continuo [a-b] debe ser continuo no debe haber una asintota de por medio

LAGRANGE

(1736-1813)

Fue quien tomo dos puntos cualesquiera a los que tambien llamo a y b e indico que la recta secante que pasa por ellos debe ser paralela ( tener la misma pendiente) que la recta tangente que pasa por un punto interior a ese intervalo. Como la pendiente de la derivada en ese valor,podemos expresar el teorema de lagrange como: